Paul Erdős (March 26, 1913 – September 20, 1996) was a prominent Hungarian mathematician. He was an extremely prolific writer (he wrote around 1,500 mathematical papers) and is famous for his excellent work in discrete mathematics, graph theory, number theory, mathematical analysis, approximation theory, set theory, and probability theory. He also contributed to the Ramsey theory. 

Robert P Langlands’ father was Robert Langlands while his mother was Kathleen Phelan. He married Charlotte Lorraine Cheverie on 13 August 1956 while he was a nineteen year old undergraduate at the University of British Columbia. He was awarded his B.A. in the following year and continued to study at the University of British Columbia for his master’s degree which was awarded in 1958. Langlands then studied at Yale University for his doctorate.

The Langlands Conjectures are of grave importance to the deep understanding of number theory and prime numbers. It has been said that Langlands possessed:

Fibonacci was born in Pisa, Italy in 1170. He played an important role in reviving ancient mathematics and made significant contributions of his own. Liber abaci introduced the Hindu-Arabic place-valued decimal system and the use of Arabic numerals into Europe.

A problem in the third section of Liber abaci  led to the introduction of the Fibonacci numbers and the Fibonacci sequence for which Fibonacci is best remembered today. The resulting sequence is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … . This sequence, in which each number is the sum of the two preceding numbers, has proved extremely fruitful and appears in many different areas of mathematics and science.

Our node is named after this famous sequence of numbers.

Nikolai Lobachevsky was born in Novgorod, Russia on 1 December 1792. He was a gifted mathematician and earned his Master’s Degree (equivalent to an American PhD) by the age of 19. He is known to be the first person to have considered a geometry where the parallel postulate does not hold – a long contested idea in mathematics.

Through his father’s encouragement Lobachevsky went on to discover hyperbolic geometry which plays an important role in theories such as relativity. Our node is name after this work. It is said of Lobachevksy that he

Borin in 836 in  Harran, Mesopotamia (now Turkey),Thabit ibn Qurra was an important Islamic mathematician who worked on number theory, astronomy and statics.

Thabit played an important role in preparing the way for such important mathematical discoveries as the extension of the concept of number to (positive) real numbers, integral calculus, theorems in spherical trigonometry, analytic geometry, and non-euclidean geometry. In astronomy Thabit was one of the first reformers of the Ptolemaic system, and in mechanics he was a founder of statics.

Bernhard Rieman was born on 17, September 1826 in Breselenz, Hanover – now Germany. His ideas concerning geometry of space had a profound effect on the development of modern theoretical physics. He clarified the notion of integral by defining what we now call the Riemann integral.

Riemann sent a report on On the number of primes less than a given magnitude, another of his great masterpieces which were to change the direction of mathematical research in a most significant way. In it Riemann examined the zeta function

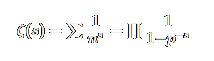
… which had already been considered by Euler. Here the sum is over all natural numbers nnn while the product is over all prime numbers. Riemann considered a very different question to the one Euler had considered, for he looked at the zeta function as a complex function rather than a real one. Except for a few trivial exceptions, the roots of ζ(s) all lie between 0 and 1. In the paper he stated that the zeta function had infinitely many nontrivial roots and that it seemed probable that they all have real part ½ ​. This is the famous Riemann hypothesis which remains today one of the most important of the unsolved problems of mathematics.

He studied the Riemann zeta function, and its extension to arbitrary number fields, discovering important results. He used these results to simplify theorems in class field theory. He then introduced the new concept of “Grössencharakter” and the corresponding L-series, to which he extended the properties of analytic continuation he had proved for the zeta functions in 1917. He discovered the decomposition laws for the divisors of discriminants for class fields.

Probably Hecke’s most important work was in 1936 with his discovery of the properties of the algebra of Hecke operators and of the Euler products associated with them. He

Erwin Schrödinger was born on 12 August 1887 in  Vienna, Austria. He made important contributions to the development of Quantum Mechanics and received a Nobel prize in 1933.

His most seminal work came as he published his revolutionary work on wave mechanics which describes the state of quantum mechanics as a wave equation. Wave mechanics, as proposed by Schrödinger in these papers, was the second formulation of quantum theory, the first being matrix mechanics due to Heisenberg – notably the Heisenberg uncertainty principle. The relation between the two formulations of wave mechanics and matrix mechanics was understood by Schrödinger immediately.

The most famous corollary of the wave equation is what is known as Schrödinger’s Cat – notably that a photon can be in many states simultaneously until observed, i.e., the cat is both alive and dead until we observe it. This node is named for this theory. It has been said of his work by many contemporaries in the field that:

 … epoch-making work.

    … the idea of your work springs from true genius…

Igor was born on 3 June 1923 in  Zhytomyr, Ukraine. Hailed as the foremost Russian mathematician of the 20th century, Igor had many other interests besides mathematics. Up until the age of 12, Igor fell passionately in love with history and classic literature – which continued thorughout his life. It was only until he turned 12 years old that signs of a gifted mathematician were eminent. 

Shafarevich made fundamental contributions to several parts of mathematics including algebraic number theory, algebraic geometry and arithmetic algebraic geometry. In algebraic number theory, the Shafarevich–Weil theorem extends the commutative reciprocity map to the case of Galois groups, which are extensions of abelian groups by finite groups.

He also was also active in Soviet politics and belonged to the same activist group that the infamous Aleksandr Solzhenitsyn lead. His political interests caused undue stress during the middle-later years of his life.

The node is named after the Galois cohomology group which illuminates properties of elliptic curves over p-adic number fields. 

Julius Petersen was in Soro, Denmark on 16 June, 1839. He was a Danish mathematician who worked on geometry and graph theory. He is best remembered for the Petersen graph. His research was on a wide variety of topics from algebra and number theory to geometry, analysis, differential equations and mechanics. He published The theory of algebraic equations in 1877 which was written in a concise style, treating as many topics as possible without using Galois theory.

He also wrote on mathematical physics, mathematical economics and a pamphlet on cryptography. His work on economics began in 1871 with the publication of a pamphlet investigating how goods could be redistributed to favour workers.

… the first major graph-theoretical paper, not only in size but also in significance.

Julio Garavito was born in Bogotá, Colombia on 5 January 1865. For his first mathematics thesis, he proposed a probabilistic approach to calculating π, while for his second, he calculated all the mathematical possibilities that a pressure gauge could have. In his final thesis, this one in engineering, Julio Garavito proposed a triangular structure to build bridges just like the Sydney Harbour Bridge.

His first thesis was title El Juego de la Aguja (The Game of Needles) and the node is named after this paper.

Fan Rong K Chung was born 9 October 1949 in Kaohsiung, Taiwan. Her interests are wide and among her nearly 200 publications there are contributions to spectral graph theory, extremal graphs, graph labelling, graph decompositions, random graphs, graph algorithms, parallel structures and various applications of graph theory in Internet computing, communication networks, software reliability, and discrete geometry. In 1997 the American Mathematical Society published a major book Spectral graph theory by Chung.

Chung and Graham were not only associated with Erdős through his mathematics, but they also were close personal friends with their home providing for him the only place he had as a base.

Her outstanding work in mathematics deserves wider recognition and our node represents her achievements.

Henri Poincaré, in full Jules Henri Poincaré, (born April 29, 1854, Nancy, France—died July 17, 1912, Paris), French mathematician, one of the greatest mathematicians and mathematical physicists at the end of 19th century. He made a series of profound innovations in geometry, the theory of differential equations, electromagnetism, topology, and the philosophy of mathematics.

His famous conjecture, the Poincaré Conjecture, was finally solved, by Russian mathematician Grigori Yakovlevich Perelman, in 2006. 

Georg Cantor, in full Georg Ferdinand Ludwig Philipp Cantor, (born March 3, 1845, St. Petersburg, Russia—died January 6, 1918, Halle, Germany), German mathematician who founded set theory and introduced the mathematically meaningful concept of transfinite numbers, indefinitely large but distinct from one another.

He spent numerous years in insane asylums most due to the lack of his acceptance of himself and his work by others in the society.

Goro Shimura born on 23 February 1930 in  Hamamatsu, Japan and is one of the most important mathematicians of the 20th century. He studied under the famous Iwasawa and is most known for his conjecture, the Taniyama-Shimura Conjecture which was the foundation in Andrew Wile’s proof of Fermat’s Last Theorem. Vaguely, the conjecture (now Theorem) surmised that every elliptic curve is modular. A bold claim that proved extremely fruitful 40 years later. 

His work in algebraic geometry is what our node is named after, particularly the Shimura Variety. It was said of Shimura that

… his important and extensive work on arithmetical geometry and automorphic forms; concepts introduced by him were often seminal, and fertile ground for new developments, as witnessed by the many notations in number theory that carry his name and that have long been familiar to workers in the field.

Jakob Bernoulli, (born January 6, 1655 [December 27, 1654, Old Style], Basel, Switzerland—died August 16, 1705, Basel), first of the Bernoulli family of Swiss mathematicians. He introduced the first principles of the calculus of variation. Bernoulli numbers, a concept that he developed, were named for him.

He is also claimed as a prominent mathematician of the Netherlands. His brother and his son were also well-known mathematicians

Bernhard Bolzano, (born Oct. 5, 1781, Prague, Bohemia, Austrian Habsburg domain [now in Czech Republic]—died Dec. 18, 1848, Prague), Bohemian mathematician and theologian who provided a more detailed proof for the binomial theorem in 1816 and suggested the means of distinguishing between finite and infinite classes.

He is famously known for his intermediate value theorem in the studies of entry level Calculus.

Andrei Andreyevich Markov Born on 14, June 1856 in Ryazan, Russia, he is best known for his work in Probability and Stochastic processes. 

He also studied sequences of mutually dependent variables, hoping to establish the limiting laws of probability in their most general form. He proved the central limit theorem under fairly general assumptions. Markov is particularly remembered for his study of Markov chains, sequences of random variables in which the future variable is determined by the present variable but is independent of the way in which the present state arose from its predecessors. This work founded a completely new branch of probability theory and launched the theory of stochastic processes.

It was said about his work in probability that it

“…contributed to a very large extent to the transformation of the theory of probability into one of the most perfected areas of mathematics.”

Theodor Molien was born on 10, September 1861 in Riga, Russia (now Latvia) and studied associative algebras and polynomial invariants of finite groups.

Molien studied Frobenius’s work on character theory (as Frobenius had studied the work of Molien) and used it to study polynomial invariants of finite groups. Molien studied how many times a given irreducible representation of a finite group appears in a complete reduction of the representation of the group on the vector space of homogeneous polynomials of degree n over the complex numbers. He gave a generating function to compute the number of times the irreducible character occurs in 1898, known as the Molien Series

The great female mathematician Emmy Noether is quoted as saying about Molien:

Fritz Zwicky born on 14 February 1898 in Varna, Bulgaria,  was a Bulgarian-born Swiss astronomer who worked most of his life in the USA. He made important contributions in theoretical and observational astronomy.

His study of galaxy clusters lead him on a very interesting discovery. While many of his statistical figures were meager in comparison to today’s analysis, this study lead to him being called “The Father of Dark Matter”

It was later said of Zwicky that

“…He pursued an extraordinary range of personal interests: international charities, city-planning, mountain climbing, new explosives, exploding stars, crystals and dying stars, and, especially galaxies. He always saw the Universe in his own original way; he loved the extraordinary objects it contained, and he explained them in his own fashion, sometimes wrong but never dull.”